電子関係の計算式も簡単だ！ 計算式は難しい！！ 　電子キットを作るだけでは計算式を学ぶ必要はありませんが、ここはチョット電子の一般常識？として考えてください。但し難しくする気はありませんので参考程度に集めて見ましたのであしからず・・・ 　電子関係で良く出てくる計算式がありますが、難しくしてもいやになるので簡単に説明します。 ・オームの法則、電力の計算、周波数の計算など、キットには関係ないかもしれませんが豆知識として・・・。 キットの回路の中にはここで紹介した公式が使われているかも…

☆　目次　☆　部品の値の読み方を調べよう！ 電子工作上どうしても出てくる法則である「オームの法則」です。 　何を計算するか調べてみましょう。 オームの法則とのつながりでワットの公式があります。 　オームの法則と合わせて調べてみましょう。 合成抵抗の抵抗値を求めましょう。 何種類かの抵抗が複雑につないであってもこの公式でバッチリです。 周波数に関する公式をまとめてみました。 　まだ公式の数は少ないのですが参考に！　チョット難しいかも知れませんが… 電子工作関係では見慣れない単位が出てきます。 　身近に使われている単位と合わせて調べてみましょう。 公式には色々な単位が出てきますがその由来について学んでみましょう。

オームの法則 　オームの法則でなんだろう？ 　抵抗の単位でオームが出てきましたが当然ながら「オームの法則」がでてきますので簡単に説明しましょう。抵抗は電流を妨げる量をオームで表現していますが実際に電圧・電流・オームの間には密接な関係がありますが、これがオームの法則です

あまり難しいこと言ってもしょうがないのでまず計算式は 　Ａ（電流・アンペア）＝Ｖ（電圧・ボルト）／Ｒ（抵抗値・オーム） 　この計算式を言葉で表現すると「１Ωの抵抗に１Ｖの電圧をかけた時に流れる電流を求める公式ですこの場合は電流は１Ａです」と言うことです。なんだかわかりづらいですが電圧が一定でオーム数が大きくなると比例して電流も減ることがわかりましたでしょうか？ 　下の表はＶ，Ａ，Ｒのそれぞれの関係を式に表した式です。

計算値 計算式 詳　　　　細 電流 Ａ＝Ｖ／Ｒ 　電圧と抵抗値がわかっている場合 電圧 Ｖ＝ＡｘＲ 　電流と抵抗値がわかっている場合にこの計算式で算出できる。 抵抗 Ｒ＝Ｖ／Ａ 　電圧と電流値がわかっている場合

＜参考＞ 　日本のはコンセント電圧は何ボルトでしょう？　　　　　１００Ｖです。　（周波数が地域によって５０Ｈｚと６０Ｈｚの２種類があります） ちなみにアメリカは１２０Ｖ／６０Ｈｚ、イギリスは２３０Ｖ／５０Ｈｚ、オーストラリアは２４０Ｖ／５０Ｈｚ、中国は１１０Ｖ・２２０Ｖ／５０Ｈｚなどです。 最近は１００Ｖから２００Ｖへ移行している国が多いようですね、どうも日本が１００Ｖと一番低い方ではないでしょうか？ このように世界各国で電源が違いますので海外旅行に持っていく電化製品には注意が必要です。 　こんな感じで世界の電圧事情を調べてみましょう。

電力について 　電力の公式でなんだろう？ 　電子キットを作る上で必ず耳にする単位があります。それはＶ（電圧）、Ａ（電流）、Ｗ（電力）です。もちろん家庭の電化製品やブレーカのアンペアなど結構家庭の周りにも使われていますので再認識してみてください。

あまり難しいこと言ってもしょうがないのでまず計算式は 　Ｗ（電力・ワット）＝Ｖ（電圧・ボルト）　ｘ　Ａ（電流・アンペア） この計算式を言葉で表現すると「１Ｖの電圧をかけた時に１Ａの電流が流れた状態の時の電力を１Ｗとする」と言うことです。なんだかわかりづらいですが１００Ｗの電球は１００Ｖで１Ａ流れていることです。 　　下の表はＷ，Ｖ，Ａのそれぞれの関係を式に表した式です。

計算値 計算式 詳　　　　細 電力 Ｗ＝ＶｘＡ 　電流と抵抗値がわかっている場合にこの計算式で算出できる。 電圧 Ｖ＝Ｗ／Ａ 　電圧と抵抗値がわかっている場合 電流 Ａ＝Ｗ／Ｖ 　電圧と電流値がわかっている場合

＜参考＞ 　６０Ｗの電球の電流はいくらでしょう？　　　　　６０Ｗ／１００Ｖ　＝０．６Ａです。 　１ＫＷの電子レンジの電流はいくらでしょう？　１０００Ｗ（１ＫＷ）／１００Ｖ＝１０Ａです。 こんな感じで身の回りの電化製品を調べてみましょう。

オームの法則と電力の公式をドッキング

■　オームの法則を・・・　■ 　上記でオームの法則と電力の公式を組み合わせると次の式で表すことができます。参考にしてみて下さい。

算出値 計算式 詳　　　　細 電力（電圧） Ｗ＝Ｖ２／Ｒ 　電流と抵抗値がわかっている場合にこの計算式で算出できる。 電力（電流） Ｗ＝Ａ２ｘＲ 　電圧と抵抗値がわかっている場合

抵抗に関する計算してみましょう。

■　実際に例題で計算してみましょう。　■ 　オームの法則の問題をそれぞれ作ってみましょう。参考になれば… ＜問題１＞　電圧Ｖ＝３．３Ｖで電流Ａ＝１０ｍＡが抵抗に流れている時の抵抗値と電力を求めよ？ ＜回答＞　抵抗値を求めるので「Ｒ＝Ｖ／Ａ」で計算しますＲ＝５Ｖ／１５ｍＡ＝０．３３Ωはまちがい！ この場合単位を合わせますが電流が「ｍＡ」ですので「Ａ」にしましょう。 　単位をＶ，Ａにした場合　　　　３．３Ｖ／０．０１Ａ＝３３０Ω 　単位をｍＶ、ｍＡにした場合　３３００ｍＶ／１０ｍＡ＝３３０Ω 次に電力を求めます。式は「Ｗ＝ＶｘＡ」です。この場合単位は必ず「Ｖ，Ａ」に合わせていきます。 　単位をＶ，Ａにする　　　　　　３．３Ｖ　ｘ　０．０１Ａ＝０．０３３Ｗ（３３ｍＷ） ＜問題２＞　電圧Ｖ＝５Ｖで抵抗４．７ＫΩの抵抗に流れている電流と電力を求めよ？ ＜回答＞　電流値を求めるので「Ａ＝Ｖ／Ｒ」で計算しますＲ＝５Ｖ／４．７ＫΩ＝１．０６Ａはまちがい！ この場合単位を合わせますが電流が「ＫΩ」ですので「Ω」にしましょう。 　単位をＶ，Ωにした場合　　　５Ｖ／４７００Ω　＝　０．００１０６Ａ（１．０６ｍＡ） 　単位をｋＶ、ｋΩにした場合　０．００５ｋＶ／４．７ＫΩ　＝　０．００１０６Ａ　こんな計算は無理ですね 　ちょっと横着した場合　　　　５Ｖ／４．７ＫΩ　＝　１．０６ｍＡ　答えがｍＡで出せます。 次に電力を求めます。式は「Ｗ＝ＶｘＡ」です。この場合単位は必ず「Ｖ，Ａ」に合わせていきます。 　単位をＡ，Ｖにする　　　　　　５Ｖ　ｘ　０．００１０６Ａ　＝　０．００５３Ｗ（５．３ｍＷ） ＜問題３＞　電流Ａ＝０．２Ａ流れる抵抗１００Ωがあります、この抵抗にかかる電圧と電力を求めよ？ ＜回答＞　電流値を求めるので「Ｖ＝Ａ　ｘ　Ｒ」で計算しますＶ＝０．３Ａ　ｘ　１００Ωとなります。 この場合単位は合っていますのでそのまま計算しましょう。（もし電流が３００ｍＡの時は０．３Ａとします） 　単位をＡ，Ωにした場合　　　０．２Ａ　ｘ　１００Ω　＝　２０Ｖ 次に電力を求めます。式は「Ｗ＝Ａ２ｘＲ」です。この場合単位は必ず「Ｖ，Ａ」に合わせていきます。 　単位をＡ，Ｖにする　　　　　　０．２２Ａ　ｘ　１００Ω　＝　４Ｗ このように計算できます。これにより抵抗の電力が４Ｗ以上必要となりますが実際は１．５倍から２倍程度必要です。 とくに電力が多い場合は２倍くらいにしましょう。ここでは１０Ｗクラスが必要でしょうか。

参考…単位を合わせるのに注意しましょう。但し値が共に同じ単位の場合はそのまま計算しましょう結果に変わりはありません。 　　初心者の方は、やはり通常の単位にして計算した方が無難でしょう。 参考…単位ですが「ｋ」は1000倍、「Ｍ」は1000000倍することで単位が変換できます。但し「０」の数がやたら増えるので間違えないでね！

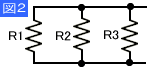
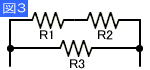
合成抵抗について 　抵抗を直列と並列にするとどう計算するのでしょう？ ■　こんな時にどうですか　■ 　電子キットを自分で作れるようになり、こんどはキットでなく工作本から自分で部品を選んで作るときに抵抗が手持ちに無い場合はどうしよう。 手持ちに無い場合は持っている抵抗だけで合成抵抗を利用して新しい抵抗値を作ってみましょう。 ■　実際に計算してみましょう　■ 　大まかに分けて２種類ありますが直列（シリーズ）と並列（パラレル）の接続方法があります。また両方が混ざった直並列接続もあります。

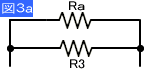
算出値 計算式 詳　　　　細 直列接続 Ｒ＝Ｒ１＋Ｒ２… 合成抵抗は抵抗をつなげた分の総和で算出できます。 並列接続 Ｒ＝　　　１　　　　＿　　 　　　１　＋　１　… 　　　　Ｒ１　　　　Ｒ２ 　合成抵抗でも並列の場合はチョット難しい式になります。 並列の場合はＲ１の逆数とＲ２の逆数の総和をまとめてから最後にもう一度逆数を求めると算出できます。 直並列接続 上記２種類を組み合わせて算出 　またまた難しいかもしれません。 計算はまず直列接続を計算し最後に並列接続を計算すれば良いでしょう。

合成抵抗を計算してみましょう。

■　実際に例題で計算してみましょう。　■ 　直列抵抗、並列抵抗、直列並列抵抗の問題をそれぞれ作ってみましょう。参考になれば… ＜問題１＞　図１でＲ１＝１ＫΩ、Ｒ２＝４７Ω、Ｒ３＝３３ＫΩの場合は合成抵抗はどのようになりますか？ ＜回答＞　直列抵抗ですのでＲ＝１ＫΩ＋４７Ω＋３３ＫΩ＝８１ｋはまちがい！ この場合単位を合わせますが今回は一番小さい抵抗値に合わせるのがやりやすいでしょう。 　単位をオームにした場合　　　　１０００Ω＋４７Ω＋３３０００Ω＝３４０４７Ω 　単位をキロオームにした場合　１ＫΩ＋０．０４７ＫΩ＋３３ＫΩ＝３４．０４７ＫΩ ※あまりこのような直列接続はしませんが抵抗値の単位を含めて出題して見ました。 ＜問題２＞　図２でＲ１＝１ＫΩ、Ｒ２＝４７Ω、Ｒ３＝３３ＫΩの場合は合成抵抗はどのようになりますか？ ＜回答＞　並列抵抗ですのでＲ＝１／（１／１ＫΩ＋１／４７Ω＋１／３３ＫΩ）＝０．９５ｋはまちがい！ この場合も単位を合わせましょう。今回も問１と同じように単位をオームにして計算してみましょう。 　１／（１／１０００Ω＋１／４７Ω＋１／３３０００Ω）＝４４．８２９Ω（４４．８Ω）となります。 上の式は次のように計算します。（計算機があると便利） 　カッコ内の逆数を計算　1/1000=0.001、1/47＝0.02127、1/33000=0.000030303　 　カッコ内の足し算　　　　（0.001＋0.02127＋0.000030303）=0.0223 　最後にもう一度逆数　　１／０．０２２３＝４４．８Ωとなります。 ＜問題３＞　図３でＲ１＝１ＫΩ、Ｒ２＝４７Ω、Ｒ３＝３３ＫΩの場合は合成抵抗はどのようになりますか？ ＜回答＞　チョット複雑ですが順番を守って計算すると解りやすいでしょう。 この場合はまず直列抵抗を計算しその後並列抵抗を計算しますと次の式になりますがカッコだらけです。 　１／（１／（１０００＋４７）＋１／３３０００）＝１０１４．８Ωとなります。 　　上の式ですとカッコが多くて難しので簡単に説明しましょう。 直列抵抗であるＲ１とＲ２を計算してＲａとします。単位はオームにしましょう。 　直列抵抗の計算　Ｒa＝（１０００Ω）１ＫΩ＋４７Ω＝１０４７Ω 直列抵抗は計算され図３ａのように並列抵抗だけになりました後は問題２のように計算します。 このでも単位は同じにするためオームにしましょう。「１／（１／Ｒａ＋１／Ｒ３）」を計算するので 　並列抵抗の計算　１／（１／１０４７Ω＋１／３３０００Ω）＝１０１４．８Ω

参考…単位を合わせるのに注意しましょう。但し抵抗値が共に同じ単位の場合はそのまま計算しましょう結果も同じ単位で扱えますし解りやすいでしょう。 　参考…並列抵抗で同じ抵抗値を２個つないだ場合は、いちいち計算するのは面倒ですが実際は簡単ですので覚えておくと便利です。２個の同じ抵抗値の場合は必ず半分の抵抗値となります。（誤差は無視しますが…） 　例…２個の１Ｋを並列接続した場合は５００Ωとなります。１０Ｋだと５Ｋ、１０Ωだと５Ωという感じです。 　参考…並列抵抗で同じ抵抗値の場合は２個で半分（１／２）で３個→１／３、４個→１／４というふうになります。

周波数の公式 　周波数ってなんだろう？ 　周波数は何でしょう。基本的には１秒間に繰り返される波の数を周波数と言うようです。身近な物では「音」・「ラジオの電波」・「テレビの電波」・「衛星放送の電波」など周波数がからんでいるものは結構たくさんあります。それぞれに周波数の範囲が割り当てられています。電波のようにＬ、Ｃを使用する場合はどうしてもこの公式が必要でしょう。 　ここでは周波数に関係する計算式を並べてみました。

共振周波数を求めよう　　ｆ＝１／２π√ＬＣ

この計算式を見るとなんだか「π（パイ）」という記号がありますね、なんでこの公式に円周率が出てくるのでしょうか？ これは周波数が交流であることに関係しています。交流にＬとＣが作る回路ではどうしても遅れが出ますこの遅れを式で表現する場合に角度で表現されます。通常は一回転を３６０度と言いますよね！でも計算式上では１８０度を「π」で３６０度を「２π」と表現し計算します。

算出値 計算式 詳　　　　細 共振周波数 ｆ＝　　１　＿　 　　２π√ＬＣ Ｌ（インダクタンス「Ｈ」）とＣ（コンデンサ容量「Ｆ」によりｆ（共振周波数）を求める公式です。 インダクタンス Ｌ＝　　１　＿　 　　４π２ｆ２Ｃ　　 上記の公式を変形してＬ（インダクタンス）を求めるようにした式です。 インダクタンス Ｌ＝＿＿１＿＿＿ 　　４π２ｆ２Ｃ　　 上記の公式を変形してＬ（インダクタンス）を求めるようにした式です。 公式の説明 　（　記号単位） ・ｆ　→　共鳴周波数（Ｈｚ） ・π　→　円周率（知ってますと思いますが参考まで「3.14159 26535 89793 23846 …」です。） ・√　→　平方根（ルート）と呼び　「ＬとＣ」を掛けた数字の平方根を求めます。 　　　　　　求める場合は関数電卓が必要ですね。 ・Ｌ　→　インダクタンスと呼び　単位は「Ｈ（ヘンリー）」です。 ・Ｃ　→　コンデンサーの容量　　単位は「Ｆ（ファラッド）」です。 注意…各単位は「ｍ（ミリ）、μ（マイクロ）、ｐ（ピコ）」の付かないので変換が必要です。

コイルのイダクタンスを求めよう　　L = ｋｕＳＮ2/ｌ

実際にコイル（アンテナコイル）などを設計する上で計算である程度決めなければなりません。 そこで本当にそのような値が出るのか検証してみましょう。

算出値 計算式 詳　　　　細 コイルの 　インダクタンス L = ｋｕＳｎ2/ｌ Ｌ（インダクタンス「Ｈ」）とＣ（コンデンサ容量「Ｆ」によりｆ（共振周波数）を求める公式です。 公式の説明 　（記号単位） ・Ｌ　→　インダクタンスと呼び、単位は「Ｈ（ヘンリー）」です。 ・ｋ　→　長岡係数（コイルの直径「ｄ」と長さ「ｌ」から係数表で算出する。 　　　　　　ｄ／ｌで算出した値を表より求めます。 ・ｕ　→　真空の透磁率（４π＊１０ー７）＊比透磁率（空気≒１．０） 　　　　　　比透磁率はコアの素材で決まるそうですが空気の場合は約１．０です。 ・Ｓ　→　コイルの断面積、単位は「ｍ２（平方メートル）」（円形のコイルの場合「πｒ２」で良い） ・ｎ　→　コイルの巻数 ・ｌ　→　コイルの長さ（線材の太さ＊コイルの巻数でも良い）単位は「ｍ（メートル）」 注意…各単位は「ｍ（ミリ）、μ（マイクロ）、ｐ（ピコ）」の付かないので変換が必要です。 長岡係数表 長岡係数表はコイルの直径と長さで変わります。またコイルの形状でも変化します。 表で「ｄ／ｉ」→「コイルの直径（ｍ）／コイルの長さ（ｍ）」で求めます。 Ｄ／ｌ 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ｋ（細長いコイル） 1.0000 0.9588 0.9200 0.8838 0.8499 0.8181 0.7885 0.7609 0.7351 0.7110 ｋ（太く短いコイル） 0.0000 0.2033 0.3198 0.4053 0.4719 0.5255 0.5697 0.6067 0.6392 0.6651 Ｄ／ｌ 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0 ｋ（細長いコイル） 0.6884 0.526 0.429 0.365 0.320 0.285 0.258 0.237 0.219 0.203 ｋ（太く短いコイル） 0.6884 - - - - - - - - -

例題　製作中

単位のお話 　単位はどこまであるのでしょうか？ 　計算式でも回路図でも部品の単位でも、なんでもかんでも全ての数字のお尻には記号が必ず付いています。 実際に抵抗・コンデンサ・コイル・距離（長さ）・重量（重さ）・容積（量）などいろいろな記号を身近に使われている物もとりまぜて表にしました。 身近の単位と比べることにより、より一層わかりやすいと思いますので参考にして下さい。 ※参考→表中のマークで「●」は良く使う、「▲」たまに使う、「−」あまり使わないに分類してみました。

読み方 単位 標準値からの倍率 抵抗 （オーム） コンデンサ （ファラド） コイル （ヘンリ） 長さ （メートル） 重さ （グラム） 容積 （リットル） ヨタ Y 1E+24 − − − − − − ゼタ Z 1E+21 − − − − − − エクサ E 1E+18 − − − − − − ペタ P 1E+15 − − − − − − テラ T 1000000000000 − − − − − − ギガ G 1000000000 ● − − − − − メガ M 1000000 ● − − − − − キロ k 1000 ● − − ● ● ● ヘクト h 100 − − − − − − デカ da 10 − − − − − − 標準 1 ● ● ● ● ● ● デシ d 0.1 − − − − − − センチ c 0.01 − − − ● − − ミリ m 0.001 ● ▲ ● ● ● ● マイクロ μ 0.000001 − ● ● ▲ ▲ ▲ ナノ n 0.000000001 − ▲ − ▲ ▲ ▲ ピコ p 0.000000000001 − ● − ▲ ▲ ▲ フェムト f 0.000000000000001 − − − − − − アト a 1E-18 − − − − − − ゼプト z 1E-21 − − − − − − ヨクト y 1E-24 − − − − − −

単位の発見者 　単位には人の名前が付いています！！ ■　アンペア（Ａ)　■ 　アンペアはフランスの物理学者であるアンペールという人がアンペールの法則１と２を発見した。 この法則が今後の発展に重要でありアンペールの業績をたたえて電流の単位を「アンペア（Ａ)」と名付けたそうです。 アンペアはアンペールの英語読みだそうです。 ■　ボルト（Ｖ)　■ 　ボルトはイタリアの物理学者であるボルタという人が電池のもとになる「ボルタの電池」を発明しました。 この発明により他の発見、発明につながったため、これらの業績をたたえ電圧の単位を「ボルト（Ｖ)」と名付けたそうです。 ■　オーム（Ω）　■ 　オームの法則はドイツの物理学者であるオームという人が発表した公式である。 その名前にちなんで抵抗の単位を「オーム（Ω）」と名付けたそうです。 ■　ヘルツ（Ｈｚ）　■ 　ヘルツはドイツの物理学者であるヘルツという人が電磁波の波（電波）をつくり出し、それを受信することに成功しました。 そこで電波の発見者であるヘルツに周波数の単位である「ヘルツ（Ｈｚ）」と名付けたそうです。 ■　ファラッド（Ｆ）　■ 　ファラッドはイギリスの物理学者、化学者であるファラデーという人が電気分解の法則、真空放電などで数多くの発見や研究をしました。 その名前にちなんで静電容量の単位を「ファラッド（Ｆ）」と名付けたそうです。 ■　クーロン（Ｃ）　■ 　クーロンはフランスの物理学者であるクーロンという人が静電気の法則を発見しました。 その名前にちなんで電気量の単位を「クーロン（Ｃ）」と名付けたそうです。 ■　ヘンリー（Ｈ）　■ 　ヘンリーはアメリカの物理学者であるヘンリーという人が強力な電磁石を開発、電磁誘導現象の発見やファラデーより先に自己誘導作用を発見したことは大きく貢献したそうです。 その名前にちなんでコイルのインダクタンスの単位を「ヘンリー（Ｈ）」と名付けたそうです。 ■　ガウス（Ｇ）　■ 　ガウスはドイツの数学者であるガウスという人が整数論、誤差論などが有名ですが小さい頃から数学の天才だったようです。 その名前にちなんで磁束密度の単位を「ガウス（Ｇ）」と名付けたそうです。 ■　ウェーバー（Ｗｂ）　■ 　ウエーバーはドイツの学校教授の息子で兄のウェーバーは人文科学、弟のウェーバーはガウスのすすめで科学者となり「ウェーバーの法則を発見しました。 その名前にちなんで磁束の単位を「ウェーバ（Ｗｂ）」と名付けたそうです。 ■　マックスウエル（Ｍｘ）　■ 　マックスウエルはイギリスの物理学者であるマックスウエルという人がファラデーの発見した法則を公式化しました。 その名前にちなんで磁束の単位を「マックスウエル（Ｍｘ）」と名付けたそうです。 　ＧとＭｘ、Ｗｂの関係式は「１Ｇ＝１Ｍｘ／ｃ�u＝１０−４Ｗｂ／�u ■　エルステッド（Ｏｅ）　■ 　エルステッドはデンマークの物理学者であるエルステッドという人が電磁気学を研究し方位磁石の針が導線に電流を流して向きを変える現象は有名です。 その名前にちなんで磁界（場）の強さの単位を「エルスデッド（Ｏｅ）」と名付けたそうです。 ■　長岡係数　■ 　長岡係数とは、物理学者であった長岡半太郎博士によって計算された係数でコイルのインダクタンスを求めれるときに使います。 コンピュータを使用すると計算も可能ですが複雑な計算なので通常は表を使って求めるようです。

空き部屋 　空き部屋 ■　空き部屋　■